2. Методика теплового расчета

По характеру теплового расчета следует различать одно- и многотрубные подземные теплопроводы. В однотрубных теплопроводах все термические сопротивления включены последовательно. В многотрубных теплопроводах все термические сопротивления включены параллельно друг другу и последовательно к цепи канал — грунт.
Однотрубный теплопровод
При бесканальной прокладке термическое сопротивление теплопровода представляет собой сумму двух слагаемых — сопротивления слоя изоляции и сопротивления грунта (см. рис. 1):
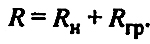 (23) (23)
При наличии воздушной прослойки между изолированным трубопроводом и стенкой канала термическое сопротивление теплопровода определяется как сумма последовательно соединенных сопротивлений (рис. 2):
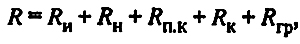 (24) (24)
где Rи, Rн, Rп.к, Rк, Rгр — сопротивление соответственно слоя изоляции, наружной поверхности изоляции, внутренней поверхности канала, стенок канала, грунта.
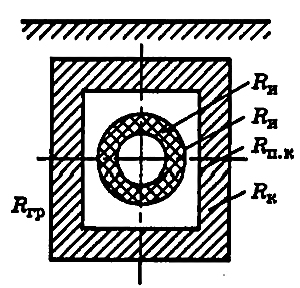
Рис. 2. Схема однотрубного теплопровода в канале
Определим температуру воздуха в канале однотрубного теплопровода. Составим уравнение теплового баланса. Количество теплоты, подведенной от теплоносителя к каналу, равно количеству теплоты, отведенной из канала в грунт:
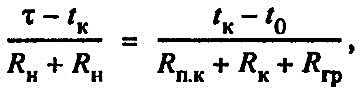
откуда:
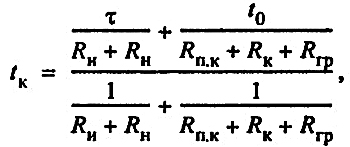 (25) (25)
где tK — температура воздуха в канале.
При изменении температуры теплоносителя на dτ температура в канале изменяется на dtK.
Из (25) следует, что
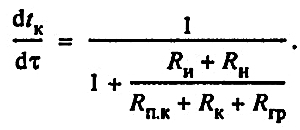 (26) (26)
Изменение температуры теплоносителя вызывает тем меньшее изменение температуры воздуха в канале, чем больше термическое сопротивление изоляционной конструкции (Rи + RH) и чем меньше термическое сопротивление канала и грунта (Rп.к + Rк +Rгр). При (Rи + Rн) = ∞, dtк = 0;
при (Rи + RH) = 0, dtK = dτ.
Многотрубный теплопровод.
Если несколько трубопроводов проложены в общем канале, то тепловой поток (тепловые потери) от каждого из них поступают в канал, а затем общий тепловой поток отводится через стенки канала и грунт в наружную среду.
Задача теплового расчета многотрубного теплопровода в канале сводится в первую очередь к нахождению температуры воздуха в канале. Зная температуру воздуха в канале, можно определить теплопотерю каждого трубопровода по общим правилам теплового расчета трубопроводов, окруженных воздухом.
Температура воздуха в канале определяется по уравнению теплового баланса. При установившемся тепловом состоянии количество теплоты, подводимой от трубопроводов к воздушной прослойке канала, равно количеству теплоты, отводимой от воздушной прослойки через стенки канала и массив грунта в окружающую среду.
Выведем основные расчетные уравнения для многотрубного теплопровода в канале. В подземном канале проложено n трубопроводов, термические сопротивления изоляционной конструкции (слоя и наружной поверхности изоляции) каждого из теплопроводов соответственно равны R1, R2,…,Rn, а температуры теплоносителя в каждом из трубопроводов τ1, τ2,…, τn.
Суммарное термическое сопротивление внутренней поверхности канала, стенок канала и грунта Rк-0 = Rп.к + RК + Rгр.
Температура грунта на глубине заложения оси теплопровода равна t0. Обозначив искомую температуру воздуха в канале через tк, напишем уравнение теплового баланса:
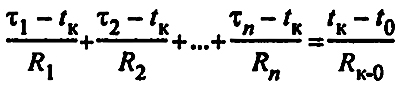 (27) (27)
откуда температура воздуха в канале многотрубного теплопровода:
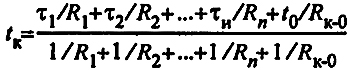 (28) (28)
Зная температуру воздуха в канале, легко найти теплопотери каждого трубопровода.
Изменение температуры любого теплоносителя (например, τ1 на dτ1 вызывает изменение температуры в канале на:
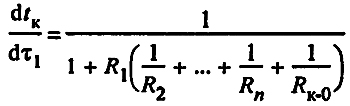 (29) (29)
Значение dtк тем меньше, чем больше тепловое сопротивление R1 и чем меньше тепловое сопротивление изоляционных конструкций остальных трубопроводов и канала. При R1 = ∞ dtK = 0; при R1 = ∞ dtK = dτ1.
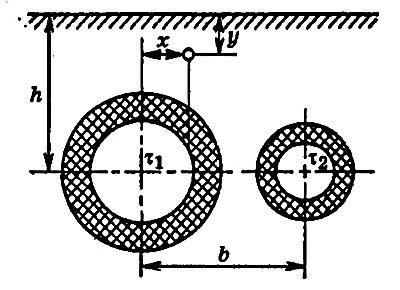
Рис. 3. Схема двухтрубного бесканального теплопровода
Расчет теплопотерь многотрубного бесканального теплопровода может быть проведен по методу, разработанному Е.П. Шубиным [148, 149]. Взаимное влияние соседних труб учитывается условным дополнительным сопротивлением R0. При двухтрубном теплопроводе условное дополнительное сопротивление (рис.3)
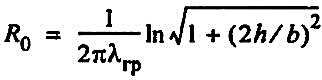 (30) (30)
где h — глубина заложения оси теплопровода от поверхности земли; Ь — расстояние по горизонтали между осями труб.
Теплопотери двухтрубного бесканального теплопровода рассчитываются по следующим формулам:
теплопотери первой трубы:
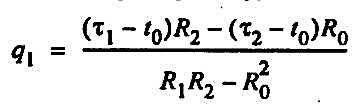 (31) (31)
теплопотери второй трубы:
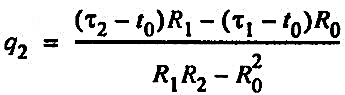 (32) (32)
где τ1 и τ2 — температуры теплоносителя в первой и второй трубах; t0 — естественная температура грунта на глубине оси теплопровода; R1 — суммарное термическое сопротивление изоляции первой трубы и грунта: R1 = Rи1 + Rгр; R2 — суммарное термическое сопротивление изоляции второй трубы и грунта: R2 = Rи2 + Rгр.
Температурное поле в грунте вокруг однотрубного бесканального теплопровода рассчитывается по формуле:
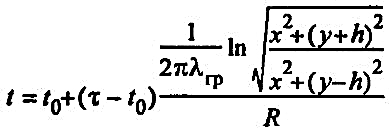 (33) (33)
где t — температура любой точки грунта, удаленной на расстояние Х от вертикальной плоскости, проходящей через ось теплопровода, и на расстояние Y от поверхности грунта, °С (см. рис. 1); τ — температура теплоносителя, °С; R — суммарное термическое сопротивление тепловой изоляции и грунта.
Температурное поле в грунте вокруг двухтрубного бесканального теплопровода вычисляется по формуле:
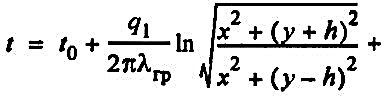
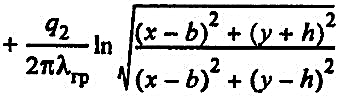 (34) (34)
где t — температура любой точки грунта, удаленной на расстояние X от вертикальной плоскости, проходящей через ось трубы с более высокой температурой теплоносителя (в двухтрубных водяных сетях — через ось подающей трубы), и на расстояние Y от поверхности грунта, °С (см. рис. 3).
Расчет температурного поля в грунте вокруг теплопровода в канале с воздушным зазором может проводиться по (33). В этом случае под τ следует понимать температуру воздуха в канале, а под R — суммарное термическое сопротивление внутренней поверхности, стенок канала и грунта.
Тепловые потери и коэффициент эффективности тепловой изоляции
Тепловые потери сети слагаются из двух частей:
- теплопотерь участков трубопровода, не имеющих арматуры и фасонных частей, — линейные теплопотери;
- теплопотерь фасонных частей, арматуры, опорных конструкций, фланцев и т.д. — местные теплопотери.
Линейные тепловые потери теплопровода:
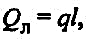 (35) (35)
где q — удельные тепловые потери, Вт/м или ккал/(ч × м); l— длина теплопровода, м.
Тепловые потери отводов, гнутых компенсаторов и других деталей, периметр поперечного сечения которых близок к периметру трубопровода, подсчитываются по формулам для прямых труб круглого сечения. Тепловые потери фланцев, фасонных частей и арматуры определяются обычно в эквивалентных длинах трубы того же диаметра:
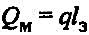 (36) (36)
где Qм — местные теплопотери, Дж/с или ккал/ч; lэ — эквивалентная длина трубы, м.
Тепловые потери от неизолированного вентиля или задвижки принимаются равными тепловым потерям изолированного трубопровода длиной 12—24 м того же диаметра при среднем качестве изоляции. Эквивалентную длину изолированного на 3/4 по верхности вентиля или задвижки в зависимости от диаметра трубопровода и температуры теплоносителя можно принимать равной 4—8 м изолированного трубопровода. Меньшие значения относятся к трубопроводу диаметром 100 мм и температуре теплоносителя 100 °С, большие — к трубопроводу диаметром 500 мм и температуре 400 °С.
Эквивалентную длину неизолированного фланца можно принимать равной 4—5 м изолированного трубопровода. Тепловые потери через неизолированные опорные конструкции теплопровода (подвески, катки, скользящие опоры) оцениваются в размере 10—15 % линейных тепловых потерь.
Суммарные тепловые потери теплопровода определяются по формуле:
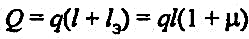 (37) (37)
где Q — суммарные тепловые потери; µ = lэ /l. Для предварительных расчетов теплопотерь теплопроводов можно принимать µ = 0,2—0,3.
Для оценки эффективности изоляционной конструкции часто пользуются показателем, называемым коэффициентом эффективности изоляции:
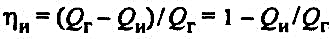 (38) (38)
где Qг, Qи — тепловые потери неизолированной и изолированной труб.
Обычно коэффициент эффективности изоляционных конструкций теплопроводов ηи = 0,85—0,95.
Падение температуры теплоносителя и выпадение конденсата
В процессе движения по теплопроводу энтальпия теплоносителя уменьшается. Вследствие этого происходит снижение температуры теплоносителя вдоль теплопровода, а при транспортировке насыщенного пара выпадает конденсат. При коротких теплопроводах, когда ожидаемое падение температуры не превышает 3—-4 % значения температуры в начале участка, расчет может проводиться в предположении постоянства удельных тепловых потерь.
Уравнение теплового баланса в этом случае имеет вид:
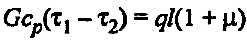 (39) (39)
где G — расход теплоносителя на участке; ср — теплоемкость теплоносителя; τ1 и τ2 — температура теплоносителя в начале и конце участка, °С; l — длина участка, м; q — удельные линейные тепловые потери; µ — коэффициент местных потерь теплоты.
Из формулы (39) следует:
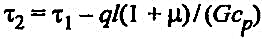 (40) (40)
При транспорте перегретого пара, когда наряду с тепловыми потерями имеют место значительные потери давления, можно пользоваться более точным методом.
По известному давлению р2 в конце участка и найденной из теплового баланса энтальпии
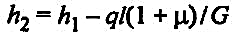 (41) (41)
с помощью таблиц или диаграмм водяного пара легко определить температуру τ2.
При длинных и слабоизолированных участках паропровода или малых расходах теплоносителя, когда ожидаемое падение температуры значительно, необходимо учитывать изменение удельных тепловых потерь по длине участка.
Рассмотрим паропровод перегретого пара длиной l. Температура пара в начале паропровода равна τ1, а в конце τ2. Окружающая среда имеет температуру t0. Термическое сопротивление изоляционной конструкции паропровода равно R. Выделим из паропровода участок бесконечно малой длины dl. Обозначим среднюю температуру пара на этом бесконечно малом участке через τ, а падение температуры пара на этом участке — через dτ. Расход пара по паропроводу равен G. Составим уравнение теплового баланса для рассматриваемого бесконечно малого участка dl с учетом местных потерь:
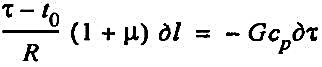
или
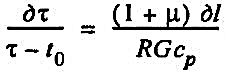 (42) (42)
Проинтегрировав формулу (42) в пределах изменения температуры от τ1 до τ2 и изменения длины паропровода от 0 до l, получим:
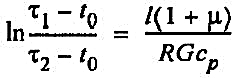 (43) (43)
Разрешая (43) относительно τ2, получаем:
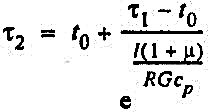 (44) (44)
Полученная формула (44), строго говоря, справедлива при изобарном процессе течения, так как при ее выводе не учитывалось падение температуры пара в паропроводе из-за падения давления.
Снижение температуры пара, вызываемое падением давления, можно определить по формуле:
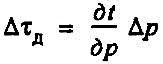 (45) (45)
где dt/dp—дифференциальный дроссель-эффект, К/Па; Δр — падение давления пара, Па.
Значение dt/dp зависит от начальных параметров пара. При давлении р1= 0,5 - 1,5 МПа и температуре перегрева τ1 = 300—350 °С дифференциальный дроссель-эффект водяного пара dt/dp = (12—14)10-6 К/Па; вблизи кривой насыщения dt/dp = (25—30)10-6 К/Па.
Действительная температура пара в конце паропровода:
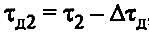 (46) (46)
где τ2 — температура пара в конце паропровода при изобарном течении, определяемая по формуле (44).
С помощью (44)—(46) можно найти длину паропровода, на которой пар теряет свой перегрев. Для точного расчета этой длины необходимо знать не только закон падения температуры вдоль паропровода, но и закон падения давления.
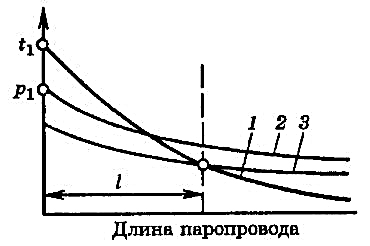
Рис. 4. Графический расчет точки насыщения
1 — изменение температуры пара; 2 — изменение
давления пара; 3 — изменение температуры насыщения
Задача решается графически (рис. 4). Построив кривую изменения температуры пара по длине паропровода 1, кривую изменения давления пара по длине паропровода 2 и кривую температур насыщения 3, соответствующую кривой давления 2, легко найти расстояние точки насыщения от начала паропровода как абсциссу точки пересечения кривых 1 и 3.
Количество конденсата, выпадающего на участке паропровода при транспортировке насыщенного пара:
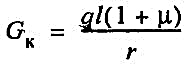 (47) (47)
где q — удельные линейные тепловые потери; l — длина участка; r — скрытая теплота парообразования.
При прекращении циркуляции теплоносителя в подземных водяных теплопроводах возникает неустановившийся тепловой процесс, при котором температура теплоносителя (воды), а также температура воздуха в канале постепенно снижаются по экспоненте, стремясь в пределе к температуре окружающей среды, которой в данном случае служит естественная температура грунта.
Пренебрегая массовыми теплоемкостями тепловой изоляции и стальной трубы, которые, как правило, значительно меньше массовой теплоемкости воды, можно определить температуру воздуха в канале подземного теплопровода через время z, с (ч), после прекращения циркуляции по формуле:
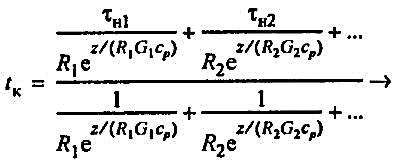
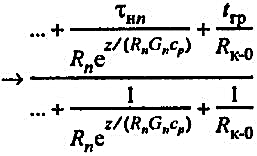 (48) (48)
где τн1, τн2,..., τn - температура теплоносителя в трубопроводах 1,2,..., n в момент прекращения циркуляции, °С; R1, R2,..., Rn - термические сопротивления изоляционной конструкции трубопроводов 1, 2, ..., n, К × м/Вт или °С × м × ч/ккал; RK-0 - термическое сопротивление канала и грунта, К × м/Вт или °C × м × ч/ккал; G1, G2, ..., Gn - масса теплоносителя в трубопроводах 1,2,..., n на единицу их длины, кг/м; ср - теплоемкость теплоносителя, Дж/(кг × К) или ккал/(кг × °С).
Температура теплоносителя в любом из трубопроводов, например в трубопроводе 1, через время z, с, (ч) после прекращения циркуляции определяется по формуле:
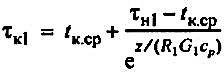 (49) (49)
где tк.ср — средняя температура воздуха в канале за период времени z, ее можно упрощенно находить по формуле tк.cp = 0,5(tкн ± tк); tкн - температура воздуха в канале в момент прекращения циркуляции; tк — то же через время z после прекращения циркуляции.
При надземной прокладке теплопроводов:
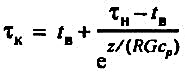 (50) (50)
где tв - температура окружающего воздуха; τн - температура теплоносителя в момент прекращения циркуляции.
Комплекс RGcp = β измеряется в секундах или часах и представляет собой по существу коэффициент тепловой аккумуляции теплопровода, аналогичный коэффициенту тепловой аккумуляции зданий.
Как следует из формулы (50)
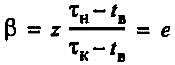
т.е. коэффициент тепловой аккумуляции теплопровода равен интервалу времени z, в течение которого при прекращении циркуляции теплоносителя температурный напор (τ - tв) изменяется в е раз.
Выбор толщины теплоизоляционного слоя
Выбор толщины изоляции определяется техническими и технико-экономическими соображениями.
Основные технические соображения, которыми руководствуются при выборе толщины изоляции, заключаются в следующем:
- обеспечение заданной температуры теплоносителя в отдельных точках тепловой сети. Это условие особенно важно для паропроводов в тех случаях, когда должна быть гарантирована подача перегретого пара отдельным абонентам;
- выдерживание нормированных экономически обоснованных теплопотерь;
- непревышение заданной температуры поверхности изоляции; при прокладке теплопровода в рабочих помещениях или в проходных каналах по условиям безопасности предельная температура поверхности должна составлять 40 °С. В некоторых случаях предельная температура поверхности выбирается из условия защиты от разрушения наружной оболочки изоляции.
На основании технических требований определяется предельная минимальная толщина тепловой изоляции. Вопрос о целесообразности увеличения толщины и повышения эффективности тепловой изоляции решается технико-экономическим расчетом.
Термическое сопротивление изоляционной конструкции трубопровода:
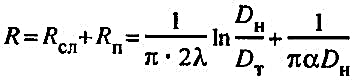 (51) (51)
При увеличении наружного диаметра изоляционной оболочки Dн термическое сопротивление слоя Rсл возрастает, а термическое сопротивление поверхности изоляции Rп снижается. При некотором значении наружного диаметра изоляции, называемом критическим Dн*, термическое сопротивление изоляционной оболочки минимально.
Это значение критического диаметра Dн*, определяемое из условия dR/dDн = О, находится по формуле:
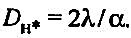 (52) (52)
Зависимость R = f(Dн) при Dт = const, λ = const и α = const показана на рис. 5.
При Dн< Dн* увеличение толщины тепловой изоляции от Dн до Dн*, дает отрицательный эффект, так как при этом тепловые потери возрастают.
В диапазоне характерных для тепловых сетей значений λ = 0,04—0,2 Вт/(м × К) и α = 6—15 Вт/(м2 × К) Dн* = 0,07—0,003 м.
Как правило, диаметры трубопроводов, применяемых в тепловых сетях, Dн > Dн*, в этих условиях увеличение толщины тепловой изоляции всегда приводит к снижению тепловых потерь.
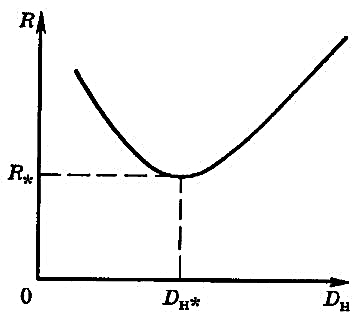
Рис. 5. Зависимость термического сопротивления от наружного диаметра изоляционной оболочки
R = f(Dн); Dт = const; λ = const; α = const
|